Biomechanical Analysis of 3-Level Anterior Cervical Discectomy and Fusion Under Physiologic Loads Using a Finite Element Model
Article information
Abstract
Objective
Pseudarthrosis and adjacent segment degeneration (ASD) are 2 common complications after multilevel anterior cervical discectomy and fusion (ACDF). We aim to identify the potential biomechanical factors contributing to pseudarthrosis and ASD following 3-level ACDF using a cervical spine finite element model (FEM).
Methods
A validated cervical spine FEM from C2 to C7 was used to study the biomechanical factors in cervical spine intervention. The FEM model was used to simulate a 3-level ACDF with intervertebral spacers and anterior cervical plating with screw fixation from C4 to C7. The model was then constrained at the inferior nodes of the T1 vertebra, and physiological loads were applied at the top vertebra. The pure moment load of 2 Nm was applied in flexion, extension, and lateral bending. A follower axial force of 75 N was applied to reproduce the weight of the cranium and muscle force, was applied using standard procedures. The motion-controlled hybrid protocol was utilized to comprehend the adjustments in the spinal biomechanics.
Results
Our cervical spine FEM demonstrated that the cranial adjacent level (C3–4) had significantly more increase in range of motion (ROM) (+90.38%) compared to the caudal adjacent level at C7–T1 (+70.18%) after C4–7 ACDF, indicating that the cranial adjacent level has more compensatory increase in ROM than the caudal adjacent level, potentially predisposing it to earlier ASD. Within the C4–7 ACDF construct, the C6–7 level had the least robust fixation during fixation compared to C4–5 and C5–6, as reflected by the smallest reduction in ROM compared to intact spine (-71.30% vs. -76.36% and -77.05%, respectively), which potentially predisposes the C6–7 level to higher risk of pseudarthrosis.
Conclusion
Biomechanical analysis of C4–7 ACDF construct using a validated cervical spine FEM indicated that the C3–4 has more compensatory increase in ROM compared to C7–T1, and C6–7 has the least robust fixation under physiological loads. These findings can help spine surgeons to predicate the areas with higher risks of pseudarthrosis and ASD, and thus developing corresponding strategies to mitigate these risks and provide appropriate preoperative counseling to patients.
INTRODUCTION
Anterior cervical discectomy and fusion (ACDF) is a “workhorse” procedure widely used to treat various cervical spine pathologies. Even though the clinical outcome of ACDF is generally favorable, postoperative complications do occur. Pseudarthrosis and adjacent segment degeneration (ASD) are 2 common issues encountered by spine surgeons after multilevel ACDF.
A recent study by Wewel et al. [1] showed that patients undergoing 3-level ACDF had a pseudarthrosis rate of 42%, whereas patients with 4-level ACDF had a pseudarthrosis rate as high as 56%. Fortunately, majority of the patients with pseudarthrosis in their series were asymptomatic, and only 11% of patients had symptomatic pseudarthrosis requiring revision surgery [1]. The author also noted that the caudal level had the most risk for pseudarthrosis in their series.
The rate of symptomatic ASD after ACDF requiring surgery has been reported to be 16% after 10 years for single-level ACDF [2], and 18% after 2-level ACDF [3]. There is not yet good long-term data on rate of symptomatic ASD requiring surgery after 3-level ACDF. However, there are some retrospective data suggesting that the radiographic rate of ASD after 3-level ACDF can be as high as 40% [4]. Given these clinical observations in the existing literature, we aim to investigate the potential biomechanical factors contributing to pseudarthrosis and ASD following 3-level ACDF using a finite element cervical spine model.
MATERIALS AND METHODS
1. Intact Spine Finite Element Model
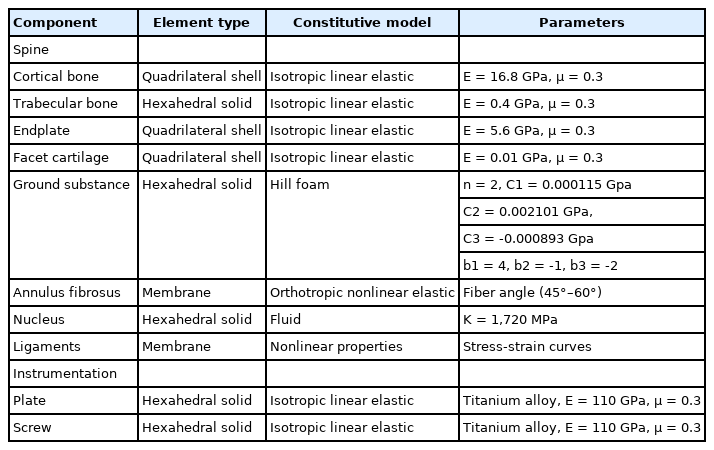
A previously validated 3-dimensional osteoligamentous finite element model (FEM) of the human subaxial cervical spinal column was used [5,6]. The FEM of the C2–T1 spinal column was assembled using a mapping block-based hexahedral meshing technique. The mesh was generated based on the geometry segmented from computed tomography images of a midsize male spine. The soft tissues definitions included intervertebral discs (annulus fibrosus and nucleus pulposus), facet joints (articular cartilage, capsular ligaments, fluid), and ligaments (anterior longitudinal, posterior longitudinal, ligamentum flavum, and interspinous). They were represented by respective element shapes and types based on their individual roles to sustain the applied external loading. The model included the C2–T1 vertebrae, intervertebral discs, and ligaments. Each vertebral body consisted of the cortical shell, cancellous bone, and superior and inferior endplates. The cortical bone (0.5 mm thick) and endplates (0.2 mm thick) were modeled as linear isotropic materials, and the cancellous bone was also modeled as an isotropic material. Intervertebral discs composed of the nucleus pulposus, and annulus ground substance and fibers. The discs had anteroposterior asymmetry simulating the posteriorly displaced nucleus in the human spine [7,8]. Annular fibers were defined using membrane elements with tension-only directional fibers embedded in the ground substance that was simulated using the Hill strain energy function. The anterior and posterior regions of the disc consisted of 16 and 8 layers. The anterior annular fibers were defined in a crisscross manner, while the posterior fibers were defined along the vertical direction. The anterior fibers did not form a continuous ring with the posterior fibers; however, a gap was formed bilaterally at the uncovertebral anatomy. The material properties of the anterior and posterior longitudinal ligaments, and other posterior ligaments were defined using nonlinear stress-strain relationships, with data obtained experimental force-displacement curves. The material properties used in the model are given in Table 1 [8-18]. A total of 11,452 finite elements were in the model with 1,392 elements at C2–3, 2,060 at C3–4, 1,970 at C4–5, 2,060 at C5–6, 2,130 at C6–7, and 1,840 at C7–T1 levels.
2. ACDF Modeling
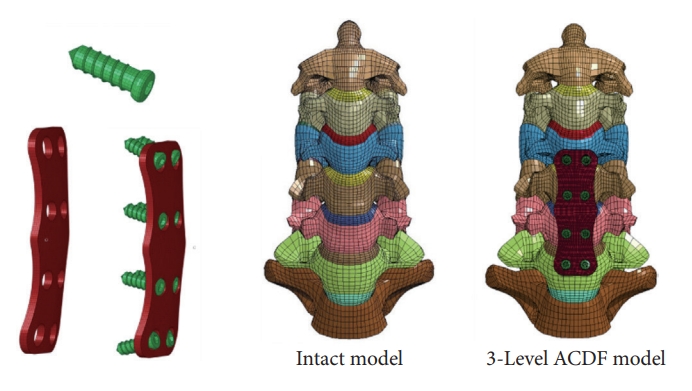
The ACDF procedure was simulated by inserting a bone graft that was placed centrally between the vertebral bodies, and material properties of the trabecular bone were assigned to the graft. A titanium plate with variable angle screws into the vertebral bodies, were simulated. The solid model of the anterior cervical plate with variable screw system was developed using CATIA V6 software (Dassault systems Corp., Velizy-Villacoublay, Cedex, France). The size of the anterior cervical plate system and variable screws were: 18 mm in length and a mean diameter of 3 mm. The solid models of the variable screws were modeled with real screw threads. The interface between the bone graft and adjacent vertebral bodies had bonded contact. After the implantation of the anterior cervical plate and screw system, the solid models were converted into the IGES format and transferred to the ANSA software and were meshed with hexahedral elements. The material properties of the instrumentation were obtained from literature (Table 1). The surface contact between the screw and vertebra was assigned with tie constraint, and between the screw and plate was assigned with automatic surface-to-surface contact definition. The intact spine was modified to simulate C4 to C7 fusion by changing the material properties of the discs to that of the cancellous bone. After graft placement at the 3 levels, a plate (height, 37.5 mm; width, 17 mm; and thickness, 2 mm) was placed along the anterior surfaces from C4 to the C7, and 2 titanium screws were simulated (Fig. 1).
3. Loading and Boundary Conditions
Both intact and ACDF FEMs of the spine were constrained at the inferior nodes of the T1 vertebra. Physiological bending moments (2 Nm) combined with a follower load (75 N) were applied (Fig. 2) [19]. First, the intact spine was exercised under flexion and extension (sagittal loading) and lateral bending modes, and the overall range of motion (ROM) was determined under each loading mode. The next step was to determine the magnitude of the bending moments to the 3-level ACDF spine that matched the ROM obtained above for the intact spine. This was done by altering the externally applied moment, under each mode, until the overall column ROM of the spine with the ACDF matched with the magnitude of the ROM of the intact spine. This is termed in literature as the hybrid loading protocol, which is described in the following section [5,6,20]. The ranges of motion at the 3 index levels and 2 cranial and caudal adjacent levels were obtained to characterize the segmental kinematics of the intact and 3-level ACDF spines. All kinematic data were normalized with respect to the intact spine and expressed as a percentage using the following equation.
Where motion represents the ROM in flexion, extension, and lateral bending, and from C2 to C7 levels.
4. Use of the Hybrid Loading Protocol
In this study, the hybrid loading protocol was used. It consisted of applying the physiological loading to the intact spine (simulating a patient’s loading paradigm preop state), extracting the overall ROM of the column, in this case C2–T1 angulation, and for the 3-level ADCF spine, determining the equivalent flexion, extension, and lateral bending moments that resulted in the same C2–T1 angulations in the 3 modes. Because of the structural differences between the intact and surgically altered spines, the moment values that match the intact spine values will be different; however, determining the segmental motions that correspond to the equivalent overall motions (of the intact and ACDF spines) from a patient perspective simulates the postop condition that can be evaluated against the preop condition. This protocol is widely used in spine finite element analyses and was adopted in this study [5,6,20].
5. Validation
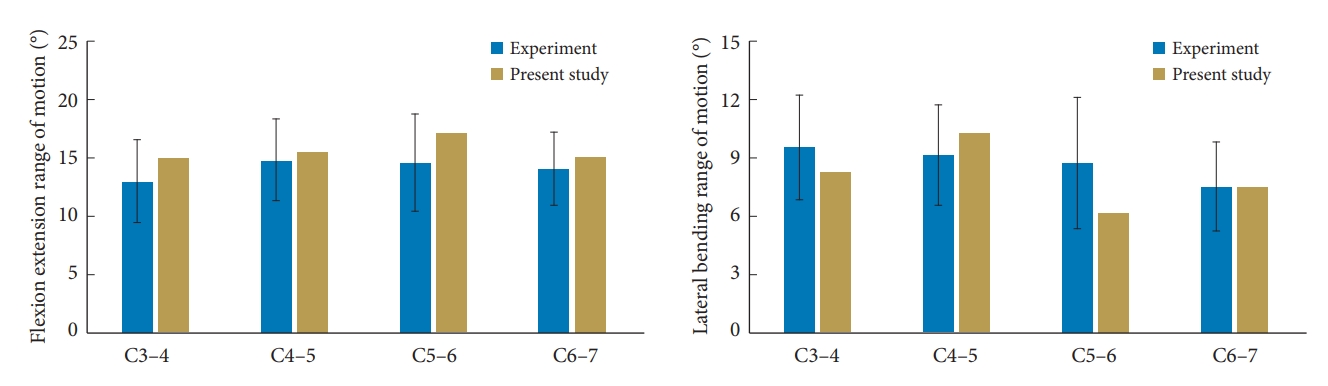
The ROM of the intact model was validated under sagittal bending by comparing the flexion-extension responses from human cadaver cervical columns that were subjected to 2 Nm of pure moment loading [21]. In the cited study, 13 spinal columns with a mean age of 33 years were subjected to 2 Nm pure moments, and the model-predicted ROM at all segmental levels for both flexion and extension were within mean ± 1 standard deviation data from experiments (Fig. 3).
Another human cadaver study was used to validate the present intact model under lateral bending [22,23]. The study used 12 spinal columns with a mean age of 62 years and applied moment of 2 Nm and follower load of 50 N. As before, the model-predicted ROM at all segmental levels were within mean ± 1 standard deviation data (Fig. 4). Similar data from human cadaver tests are not available for the 3-level ACDF spines. From this perspective, it would be necessary to conduct experiments to further validate the ACDF model. This is a topic for future investigation.
For validating the model, experimental data were available for 2 loading cases: pure moment at 2 Nm, and combined moment and force loading of 2 Nm and 50 N. Results from the 3 level ACDF were based on a greater force of 75 N (instead of 50 N), while the moment loading remained the same. The effect of 2 Nm + 75 N versus 2 Nm + 50 N loading scenarios, as measured by the difference in the ROM between the 2 load magnitudes across all levels and modes ranged from 3.9% to 5.6%, with a mean of 4.9%. Because of small differences in the modeling output, results with 75 N are considered more realistic as it better simulates muscular forces and accounts for the weight of the head on the spine.
RESULTS
After C4–7 ACDF, the mean reductions in ROM across C4–7 were -79.3%± 2.3% under flexion, -66.2%± 6.4% under extension, and -53.8%± 20.9% under lateral bending. The maximum ROM reductions were at C4–5 for flexion and C5–6 for extension.
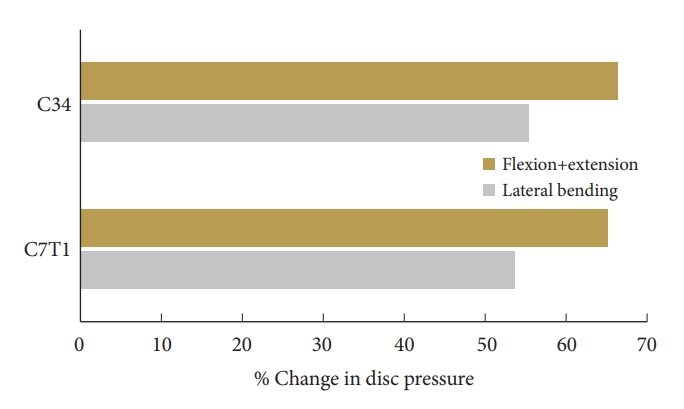
Under flexion loading, the mean increase in ROM across C2–3 and C3–4 levels were 97.0%± 9.6%, under extension loading it was 84.1% ± 9.3%, with the maximum increase at the C2–3 in the former and C3–4 in the later mode. At the caudal level, C7–T1, under flexion, extension, and lateral bending, the increase in motion was 73.8%, 64.0%, and 65.2%, respectively. Under lateral bending the mean decrease in motion across C4–7 was 57.0%± 3.3% (Fig. 5). Fig. 6 demonstrates the stress distribution on the plate-screw interface in flexion. Red areas indicate the greatest von Mises (VM) stress in the ACDF plate and the light blue regions show the least VM stress. The maximum stress in the plate was 64 MPa. disc pressure at C3–4 increased by over 59%, 74%, and 55% for the flexion, extension, and lateral bending in the 3-level ACDF when compared with intact spine and a similar trend was observed for C7–T1 (Fig. 7).

Bar charts showing the change in motion at each level. Note that the motions decrease at the 3 index levels.
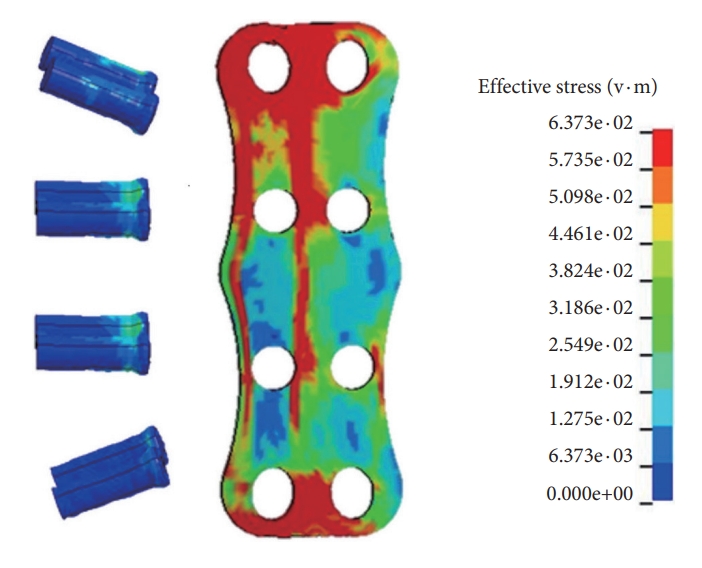
Stress distribution on the plate-screw interface in the model in flexion. Red areas indicate the greatest von Mises (VM) stress in the anterior cervical discectomy and fusion plate and the light blue regions show the least VM stress. The maximum stress in the plate was 64 MPa.
DISCUSSION
The objective of the study was to investigate the responses of the 3-level ACDF from a segmental ROM perspective and compare them to the intact spine under 3 physiological loading conditions: flexion, extension, representing sagittal bending, and lateral bending. As expected, angulations at the index levels changes in all modes of loading, with greater decreases in sagittal than coronal loading. As shown in the results section, among the 3 index levels, under combined sagittal bending moments, the least rigid segment was at the caudal level (decrease in motion -71.3%), and the cranial and middle levels had approximately same levels of decrease in range motion (-76.4% and -77.1%). In other words, the greatest and least motion reduction occurred at the middle and caudal levels, C5–6 and C6–7, respectively. While changes between the 3 levels were small and their clinical significance is not clearly established, the added mobility at the caudal segment may delay arthrodesis. Interestingly, this result mirrors a recent clinical study by Nichols et al. [24] where they found that the middle level had the highest rate of fusion, and the caudal level had the lowest rate of fusion at 24 months after 3-level ACDF. Specifically, the authors analyzed the radiographic outcome of a group of 77 patients who underwent 3-level ACDF and used flexion-extension x-rays to assess fusion status at various time points. At 6 months after surgery, they found the fusion rates were 17%, 34%, and 4% for the cranial, middle, and caudal levels, respectively; at 24 months after surgery, they rates were 61%, 89%, and 28%, respectively. The segmental fusion pattern observed in their clinical series agrees with the findings from our current FEM study.
We acknowledge that the longitudinal effects of the patient’s spine are not fully incorporated in the current finite element kinematic analysis. Despite this being a single cycle study, the present findings appear to offer support to the theory advanced by the authors in the cited study: pseudarthrosis occurrence at the caudal segment [24]. Additional studies are however, needed to fully explore the repeated loading paradigm, for which properties of the components such as the viscoelasticity of the discs and their degeneration status should be included. Preliminary data on such properties are available [25,26]. Furthermore, the present model was developed using mapping block morphing techniques [27], it should be possible to simulate the actual anatomical geometry of the patient, include appropriate material properties via computed tomography and magnetic resonance imaging, and more accurately determine the cranial, middle, and caudal level ranges of motions and estimate the rates of arthrodesis in the future.
At adjacent levels, the cranial segments (C2–3, C3–4) experienced more compensatory increase in segmental motion under load compared to the caudal level (C7-T1). This suggests that the added rigidity of the 3-level ACDF induces a nonuniform shift of the kinematics to the adjacent levels. This finding may be explained by the proximity to the head mass. The rate of adjacent segment disease will be nonuniform from this perspective, a phenomenon observed in previous retrospective studies [28,29]. In addition, Lundine et al. [30] demonstrated that the cranial adjacent level is more likely to have adjacent level degeneration compared to the caudal adjacent level, which is consistent with the findings suggested by our FEM model.
Because lateral bending is also an important physiological motion of the cervical spine, the present study investigated the responses under this loading condition as well. It should be noted at the outset that the bilateral symmetry of the structure is lost in this mode as ipsilateral facet column is under a compressive phase while the contralateral column is under a tensile phase. Acknowledging the asymmetric modality, the caudal and middle index levels responded with lesser increase in angulation than the cranial index level. This implies as greater load on the ipsilateral column at the middle and cranial levels compared to the caudal index level. A similar phenomenon also occurred at the 2 most superior adjacent levels (C2–4) when compared to the inferior (C7–T1) level. Taken together, the biomechanical responses of the 3-level ACDF spine are level-specific and motion-dependent. Our FEM study appears to offer quantitative explanations and support clinical hypothesis regarding its outcomes.
CONCLUSION
Biomechanical analysis of C4–7 ACDF construct using a validated cervical spine FEM indicated that C6–7 has the least robust fixation under physiological loads, potentially predisposing it to higher rate of pseudarthrosis. The C2–3 and C3–4 have more compensatory increase in ROM compared to C7–T1, which may imply that these levels are more prone to develop ASD over time. These findings can potentially help spine surgeons to predicate the areas with higher risks of postoperative complications and thus developing corresponding strategies to mitigate these risks and provide appropriate preoperative counseling to patients.
Notes
Conflict of Interest
The authors have nothing to disclose.
Funding/Support
This study was supported by the Office of the Assistant Secretary of Defense for Health Affairs, through the Broad Agency Announcement under Award No. W81XWH-16-1-0010 and the Department of Veterans Affairs Medical Center, Milwaukee, WI, USA.
Author Contribution
Conceptualization: LT, NY, HC, YP, DJ, AB; Data curation: LT, NY, HC, YP, DJ, AB; Formal analysis: LT, NY, HC, YP, DJ, AB; Funding acquisition: H Choi, YP; Methodology: H Choi, YP, DJ, AB; Project administration: LT, NY, HC, YP; Visualization: YP; Writing - original draft: LT, NY, HC, YP, DJ, AB; Writing - review & editing: LT, NY, HC, YP, DJ, AB.
Acknowledgements
Dr. Yoganandan is an employee of the VA Medical Center. The opinions, interpretations, and conclusions are solely from the authors.