Expressing Cobb Angle as Linear Measurement in Scoliosis and Its Significance: A Clinical and Geometrical Analysis of Scoliosis
Article information
Abstract
Objective
The aim of this study was to formulate an objective clinical and geometric relationship between Cobb angle and the difference between the lengths of convex and concave sides (convexo-concave vertebral difference) of the structural curve in scoliosis. Is it possible to express Cobb angle in such a way that it could be visualized as a length, especially while planning for surgical correction of scoliosis?
Methods
Thirty consecutive patients below the age of 19 years with a scoliosis of Cobb angle more than 10 degrees were included in the study. Convexo-concave vertebral difference of the structural curve was measured. Its relationship with the measure of Cobb angle was studied.
Results
Author obtained a significant linear correlation between the convexo-concave vertebral differences and the Cobb angle. Using the formula Y=2d.Sin (X/2) the convexo-concave vertebral difference could be predicted. The difference thus obtained gives a quantitative measure of the maximum length of correction possible in the structural curve.
Conclusion
It is possible to express the Cobb angle as a function of linear measurement. The author proposes that this would aid the surgeons to accurately and predictably achieve the desired scoliosis correction.
INTRODUCTION
The first account of treatment rendered for spinal deformity is recorded in the Srimad Bhagwat Mahapuranam, an ancient Indian epic written between 3500 and 1800 BC. A passage describes Lord Krishna applying axial traction to correct the hunchback in one of his devotees, Kubja9). We have progressed a long way forward. Bracing, posterior spinal fusion and instrumentation, anterior spinal fusion and instrumentation, thoracoscopic scoliosis surgery and fusion-less scoliosis correction are all proved methods of treating scoliosis1–5,7).
Yet, high variability in selection of both operative approach and fusion levels exist even today. Further, there were times that treating surgeons could not achieve desired corrections, even after full set of preoperative investigations, in their interventions either via posterior or anterior or combined approaches. To address these facts, investigators continue to focus on identifying better tools for the evaluation and treatment of scoliosis10).
The purpose of this article is threefold. First, it serves to establish the existence of a linear relationship between the Cobb angle and the difference in the length between the convex and concave sides (convexo-concave vertebral difference) of a structural curve in scoliosis clinically. Second, it analyzes the scoliosis geometrically, to further establish this relationship as a mathematical formulation. Third, the author proposes that the new method of expressing Cobb angle as a linear measurement can serve as tool for the evaluation of scoliosis aiding the surgeons to plan the operative approach and the fusion levels more accurately.
Research questions were as follows: (1) In patients with structural scoliosis, does a method exist to express the cobb angle as a function of linear measurement? (2) Does such an expression theoretically improve the accuracy of surgical correction of scoliosis?
MATERIALS AND METHODS
All scoliosis patients who attended the outpatient department of the Department of Orthopedics, in our institute between 2001 January and 2005 January were reviewed. The inclusion criteria in the study were: Scoliosis of more than 10° Cobb angle and patient age between 10 and 19 years. Thirty consecutive patients (24 female and 6 male patients) fit these criteria and all were available for analysis. The mean age for all patients was 13 years (range, 10–18 years). All patients were evaluated radiologically. The evaluation involved standing posterioranterior (PA) films of the entire spine. Supine bending films of all the curves were obtained to differentiate between major (structural) and the compensatory curves. Author identified that, if we measure the length of any structural curve on the convex and concave sides (Fig. 1), the convex side was longer than the concave side. This convexo-concave vertebral difference of structural curve was measured in all patients as described below. In the standing PA radiogram upper and lower end vertebrae were determined by standard method. Most clearly visible outer and uppermost point of the upper end vertebra was marked as point A. Similarly, outermost and lowermost point of the lower end vertebra was marked as point B. Straight line joining these 2 points, that is, the line AB was drawn and the length was measured in millimeters (mm). Innermost and uppermost point of the upper end vertebra was marked as point C. the distance between point A and C was measured as “d.” A point was selected on the lowermost part of the lower end vertebra that was marked as point D, so that it was inner to the point B and AC=BD. The distance between C and D was measured in millimeters (Fig. 1). Convexo-concave vertebral difference was obtained in all patients by subtracting the measure of CD from AB. Cobb angle was measured in all patients by standard method. Correlation between the convexo-concave vertebral differences and the Cobb angle was evaluated using SPSS ver. 10 (SPSS Inc., Chicago, IL, USA). A geometrical construct was made to identify any mathematical relationship that may exist between the Cobb angle and the convexo-concave vertebral difference.

Line diagram showing measurement of convexo-concave vertebral difference. Most clearly visible outer and uppermost point of the upper end vertebra was marked as point A. Similarly, outermost and lowermost point of the lower end vertebra was marked as point B. Straight line joining these 2 points, that is, the line AB was drawn and the length was measured in millimeters. Innermost and uppermost point of the upper end vertebra was marked as point C. the distance between point A and C was measured. A point was selected on the lowermost part of the lower end vertebra that was marked as point D, so that it was inner to the point B and AC=BD. The distance between C and D was measured in millimeters. Convexo-concave vertebral difference was obtained by subtracting the measure of CD from AB.
This study was approved by the Institutional Review Board of Government Medical College, Thrissur.
RESULTS
All the thirty patients were available for the evaluation. Convexo-concave vertebral difference was measured in all patients and was compared with the standard Cobb angle of the structural curve. Significant linear correlation (r=0.88) was obtained (Fig. 2). More over, it was possible to prove that this correlation can be formulated. Further, just by measuring breadth of upper end plate and knowing the Cobb angle we could calculate the corresponding convexo-concave vertebral difference.
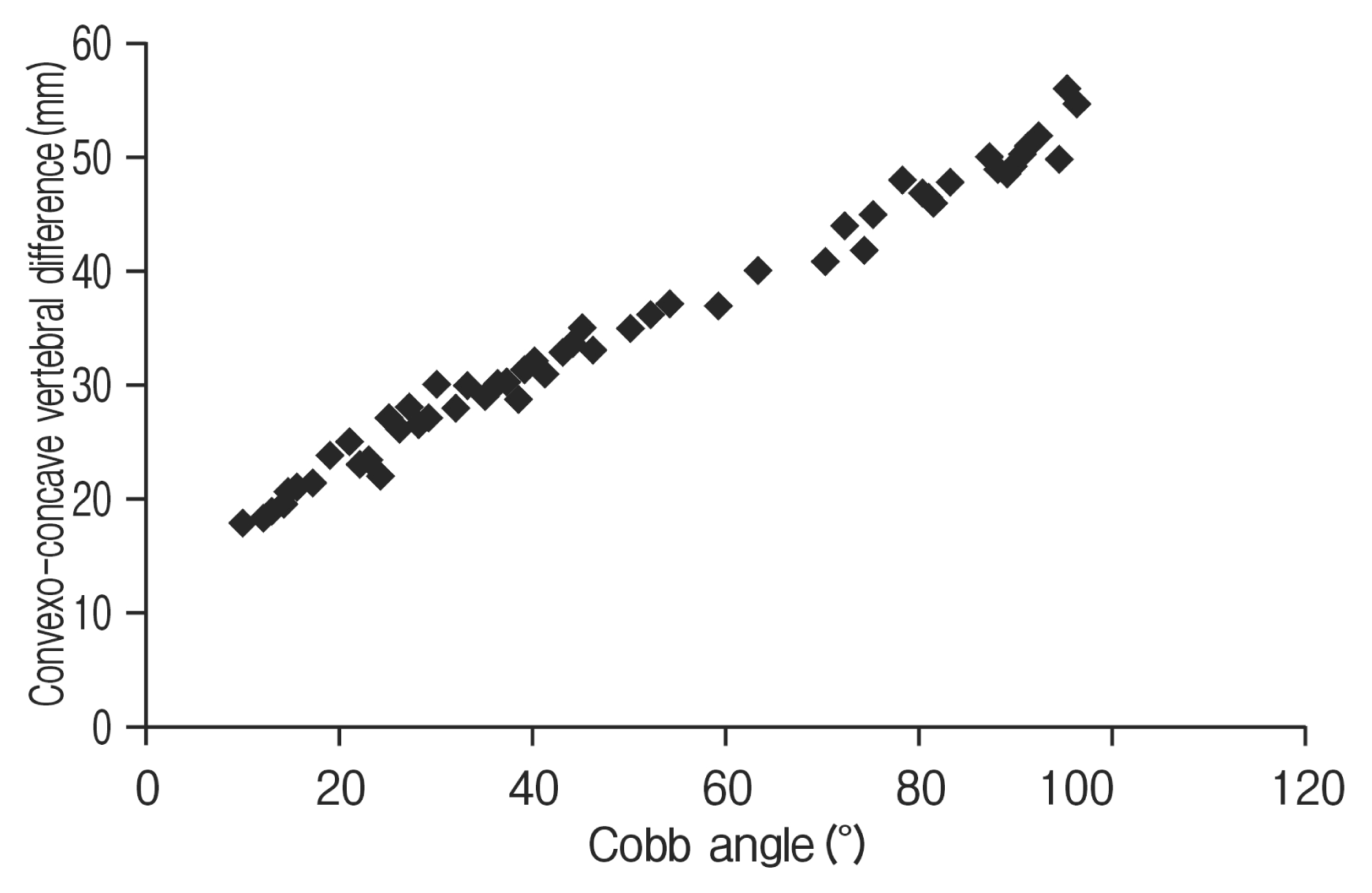
XY scatter diagram showing linear relationship between the Cobb angle (plotted on X axis) and the convexo-concave vertebral difference in millimeters (plotted on Y axis).
Difference of convex and concave sides (Convexo-concave vertebral difference) is independent of the length of scoliosis. Further (Fig. 3), though AC represents the actual breadth of upper end plate of the cranial vertebra, BD does not necessarily represent the actual breadth of defined endplate. Therefore this relationship is geometric rather than anatomic. If we draw a perpendicular line from C to line AB and define this point as A′ and do the same procedure and draw a line perpendicular to AB from D and call B′ the sum of segment AA′ and BB′ would give the convexo-concave vertebral difference (AA′=BB′). Further, if we draw virtual lines from AC and BD they would bisect at some point “E.” Angle AEB is the Cobb angle of the curve. Angle bisector of AEB is a line that is perpendicular to AB and is the height of the triangle AEB. H is the point where angle bisector meets the line AB. Now we have 2 similar triangles that is ACA′ and AEH. Angle AEH is Cobb/2 (Cobb=X). Using the principle of similar triangles we can see that ACA′ angle is also X/2. Thus AA′=AC.sin (X/2). Convexo-concave difference=AA′+BB′. Thus Y=2.d.sin (X/2) (X is the Cobb angle, Y the convexo-concave vertebral difference and d the measure of the line AC as shown in Fig. 3). This is the same linear relationship that we obtained in Fig. 2.
DISCUSSION
The deformity in scoliosis is three dimensional in nature and effective correction involves all three planes8). The long-term outcome of surgically treated scoliosis is dependent not only on the coronal correction but also on restoration of sagittal curves6,11). Vertebral rotation, sagittal imbalance, and lateral curvature are accepted as elements in scoliosis that are to be addressed separately while surgically correcting the deformity12).
Lateral curvature of scoliosis is expressed as Cobb angle traditionally12). Further, rigidity (or flexibility) of a scoliotic curve has been determined (or at least estimated) by flexibility measurements of that curve by means of x-rays taken at different forced positions such as side bending, traction, fulcrum bending or even push prone under general anesthesia. Supine bending radiographs are presently the gold standard technique by which flexibility is assessed10). The differences thus obtained in the Cobb angle before and after applying a stress is usually taken as the degree of correction attempted at the time of surgical correction. Distraction on the concave side and or compression applied on the convex side is the maneuver used to correct the lateral curvature of scoliosis12). But there were times that treating surgeons could not achieve desired corrections, even after full set of preoperative investigations, in their interventions either via posterior or anterior or combined approaches10). Author believes that this shortcoming is due to difficulty experienced by the surgeon in visualizing the proposed angle of correction per-operatively. Our method of expressing proposed degrees of correction as a length (instead of angle), addresses this to a great extent.
In this method that we describe, only Cobb angle and the lateral curvature that it represents are addressed. Quantifying the widely used derotation techniques11) in correcting vertebral rotation and sagittal imbalance in scoliosis are beyond the scope of this discussion.
If the Cobb angle of a structural curve can be made to approach 0°, it can be said that maximum correction possible in that particular curve is achieved. In that ideal situation, the difference in length of convex and the concave sides of the original structural curve will also approach zero. In other words, convexo-concave vertebral difference is a linear expression of the corresponding Cobb angle. The degree of structural correction attempted (based on stress tests) may not be equal to the maximum correction possible (Cobb angle=0°). Using the formula Y=2.d.sin (X/2), both the maximum correction possible and the maximum correction attempted can be expressed as a length. Suppose we take an example in which X is the desired angle of correction in a scoliosis. Using the formula, Y′=2.d.sin (X/2), Y′ will be the corresponding convexo-concave vertebral difference or the maximum correction attempted. Now we have a readily available length called Y′ that can be used per-operatively in the following way: If we are intervening only on the convex side of the curve, compression (shortening), “A” required for the desired correction will be equal to “Y′.” Instead if we are attempting to correct the curve by distracting (lengthening) the concave side, the amount of distraction, “B,” required for the same, will again be equal to “Y′.” If in another case, we try to correct both the convex and concave sides of the structural curve, the combined length of correction (A+B) will be equal to Y′. Thus, by expressing Cobb angle as a length, the desired correction can be objectively expressed per-operatively in a predictable manner.
In ideal situation, maximum correction of a structural curve (Cobb angle=0°) will make the spine straight. The corresponding convexo-concave vertebral difference that is to be corrected will be Y, i.e., when Y′ approaches Y the spine will become straight. By knowing this the treating surgeon will be able to quantify the maximum compression or distraction or both that can be give to a structural curve.
CONCLUSION
In conclusion, convexo-concave vertebral difference is a linear expression of the corresponding Cobb angle. But this finding should be viewed after considering the following limitation that, the study did not quantify the per-operative utility of the proposed measurement technique. Although it remains to be seen whether or not the proposed measurement will be beneficial, author strongly believe that by expressing the Cobb angle as a length, the treating surgeon can more predictably and accurately achieve the desired scoliosis correction.
Notes
CONFLICT OF INTEREST
No potential conflict of interest relevant to this article was reported.
