Oxford Cobbometer Versus Computer Assisted-Software for Measurement of Cobb Angle in Adolescent Idiopathic Scoliosis
Article information
Abstract
Objective
The objective was to compare Cobb angle measurements performed using an Oxford Cobbmeter and digital computer software (Surgimap) in a series of 83 adolescent idiopathic scoliosis (AIS) patients.
Methods
Two independent observers measured the Cobb angles for 123 curves on 83 consecutive long radiographs of patients with AIS using both Oxford Cobbmeter and digital computer software (Surgimap). The measurements were repeated a week. Curves were classified according to the severity into mild, moderate, and severe. The results were statistically analyzed for intraobserver and interobserver reliability
Results
The mean Cobb angle was 48.12° ± 19.75° (range, 10.54°–110.76°). Globally the results of curve measurements were comparable between and within both observers using both methods, with small mean differences. According to intraclass correlation coefficient, there was high inter- and intraobserver high agreement for both methods. All readings were > 0.9. There was a good interobserver (κ = 0.745, 0.693) and a very good interobserver agreement (κ = 0.810, 0.804) for both methods for curve classification. However, poor agreement was observed as regards to the measurement time, being less with Oxford Cobbometer.
Conclusion
The results of this study indicate that the Surgimap digital computer software measurement is an equivalent measuring tool to the Oxford Cobbmeter in Cobb angle measurement. Both have high intra and interobserver agreement for measurement and for curve classification, with small measurement differences. Oxford Cobbmeter is advantageous in being quicker, and therefore it is the method of choice for manual measurement, where PACS (patient archiving and communication system) or digital system is not available.
INTRODUCTION
Adolescent idiopathic scoliosis (AIS) is a 3-dimensional deformity of the spine, which is characterized by the lateral curvature of the spine and vertebral rotation [1].
Currently, Cobb angle measurement is the standard method to quantify spinal curvature [2]. The Cobb angle measures only the amount of the most tilted vertebrae on an anteriorposterior radiographs in the coronal plane and is not an objective measurement of all 3-dimensional aspects of the spinal deformity. However, this determination is important in decision-making regarding progression, and orthotic options, as well as the surgical interventions and the evaluation of treatment outcomes [3-5]. Thus, satisfactory reliability and reproducibility measuring procedures to facilitate comparison within and between studies are crucial [6].
Different methods are available to measure the Cobb angle in scoliosis. The most traditional and widely used is the protractor [7]. The Oxford Cobbometer (Oxford Orthopedic Engineering Centre, Oxford, UK) was first described in 1979 as a device to measure Cobb angles quickly and without construction lines [8]. Computer-aided methods including Patient Archiving and Communication System (PACS) are available in many centers over the world, and it facilitates Cobb angle measurement. The recent generations of mobile ‘smart phones’ with integrated clinical applications became popular in orthopedic clinics for scoliosis measurements [9-11].
Traditionally, a change of 5 degrees has been accepted as the value needed to be certain that the curve has progressed [9].
Several studies have focused on the intra- and interrater reliability of the Cobb angle measurement, with estimates from 2.8° to 10° using a 95% confidence interval (CI) [7,9,11,12].
Since some surgeons especially in the developing countries are still using manual measurements because of preference or the unavailability of PACS, the newer digital advancements to determine the Cobb angle must establish themselves as at least equivalent to the manual procedure as regards to the validity and reliability.
The purpose of the current study was to compare Oxford Cobbometer and computer software in Cobb angle measurement in AIS. To the best of our knowledge, this is the first study to compare both methods.
MATERIALS AND METHODS
1. Patients
After an appropriate Institutional Review Board approval of Alexandria University (IRB No. 131-15) was obtained, consecutive patients with AIS attending our clinic between January 2017 and May 2018 were included in this study. An informed consent was obtained from every patient. Ethics approval of this study was received. Selection criteria required that patients were 10 years or more, Cobb angle of at least 10 degrees, and had no other neuromuscular or skeletal disorders or previous spine surgery.
2. Radiographic Measurement
Two independent observers (one experienced spinal orthopedic senior consultant and one spinal fellow experienced in spinal deformities) measured the Cobb angles in standing whole spine posteroanterior radiograph. Images area ranged from occiput to the hip joints. Damaged or unclear images were excluded.
To assess inter and intraobserver variability associated with the 2 measurement techniques, the 2 observers performed a second set of measurements a week after their first set of measurements using the same radiographs to reduce the effect of memory.
Measurements using the 2 techniques were recorded on separate datasheets. The first observer was blinded to his prior measurements and to the second observer.
During measurements, the observers recorded the upper and lower end vertebrae selected for each curve. The end vertebrae were defined as the most tilted vertebra (that which subtended the greatest Cobb angle) at the cephalad and caudal ends of a curve. The end vertebrae were preselected by the senior author to reduce the component of variability.
To estimate the relative measurement time for the 2 techniques, the observers recorded the time they took to perform each radiograph.
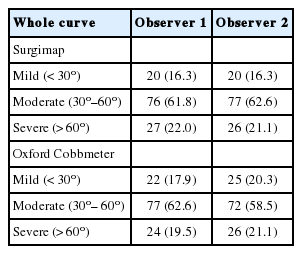
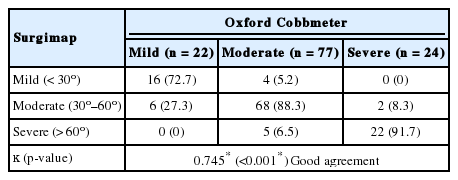
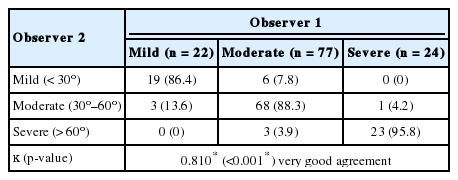
In addition, curves were classified according to the severity into mild (< 30°), moderate (30°–60°), and severe (> 60°).
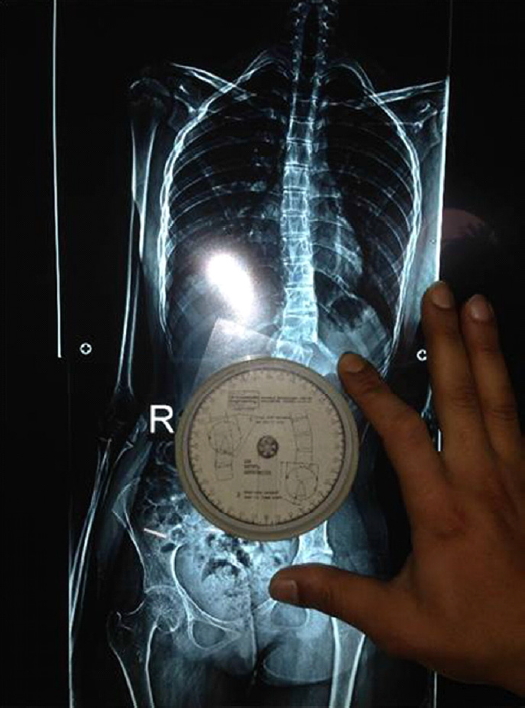
3. Oxford Cobbometer
The Oxford Cobbometer is composed of 3 parts: a clear Perspex backplate, a circular protractor calibrated from 0 to 180 in both directions, and a pendulum. The components are connected with a central spindle and encased in a clear protective cover. The components are connected with a central spindle and encased in a clear protective cover [12].
In this technique, radiographs were assessed on a vertical viewing screen. The upper edge of the Oxford Cobbmeter was applied to the upper endplate of the most tilted upper vertebra and was rotated to zero. After that, the Cobbometer was applied to the lower end plate of the most tilted lower vertebra and the angle measured is the Cobb angle [9]. If one or both endplates were not visible, the upper and lower borders of both pedicles of the upper end and lower end vertebrae respectively (pedicle method) [13] were used to make the same lines for measurement of the Cobb angle (Fig. 1).
4. Computer-Aided Cobb Angle Measurement
Surgimap Spine software (Nemaris, New York, USA) technique to measure Cobb angle is one of the most popular digital methods used to measure Cobb angle. Its reliable and reproducible measurements are critical for clinical studies [14]. For the specific software technique, all images were stored in the designated computer. The radiographs were all blinded, numbered, and viewed on the same Surgimap Spine software. Lines were drawn through the endplates of the upper and lower end vertebrae of the curve. Pedicle method was used if the endplates were not clear. The program measured the Cobb angle automatically.
5. Statistical Analysis
Data were fed to the computer and analyzed using IBM SPSS Statistics ver. 20.0 (IBM Co., Armonk, NY, USA). Qualitative data were described using number and percent. The Kolmogorov-Smirnov test was used to verify the normality of distribution. Quantitative data were described using range (minimum and maximum), mean, standard deviation and median. The significance of the obtained results was judged at the 5% level. Paired t-test was used for normally distributed quantitative variables, to compare. Bland-Altman test was used for agreement using Bland-Altman plot and 1-sample t-test. In addition, kappa (κ) test and intraclass correlation coefficient (ICC) were used for the agreement between observers. Following the recommendations by Landis and Koch for Kappa (0–0.20, poor agreement; 0.20–0.40, fair agreement; 0.40–0.60, moderate agreement; 0.60–0.80, good agreement; and 0.80–1, very good agreement) [15]. The ICC was classified using a system suggested by McGraw and Wong as follows: less than 0.75 poor agreement; 0.75 to less than 0.90 moderate agreement; 0.90 or greater high agreement [16]. Summary statistics from analysis of variance calculations were used to provide 95% prediction limits for the error in measurements. A p-value less than 0.05 was considered statistically significant.
RESULTS
1. Demographic Data
The material of this study included a total of 83 consecutive long radiographs of cases of AIS, and was evaluated on 2 separate occasions by 2 independent observers (664 data points). Sixty-five were females (78.3%) and 18 were males (21.7%), with a mean age of 15.33± 4.37 years (range, 10–35 years). The total number of curves was 123 curves (83 main thoracic and 40 lumbar). According to curves severity, moderate curves were the most frequent according to the measurements of both observes (Table 1). The mean Cobb angle was 48.12°±19.75° (range, 10.54°–110.76°).
2. Overall Results of Curve Measurement
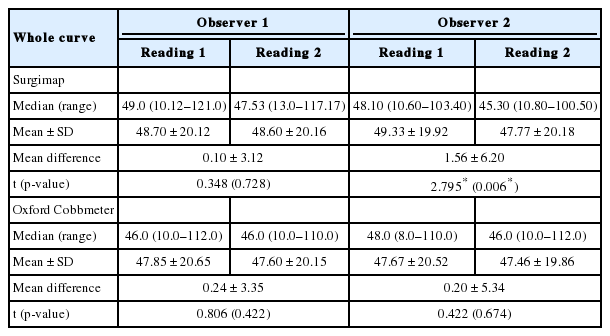
Globally the results of curve measurements using Oxford Cobbometer were comparable between and within both observers, with very small differences between readings. No statistical significance could be found. With Surgimap, also a small mean difference was found with observer 1 without a statistical significance. However, a statistical significance was noticed with observer 2 for both readings with Surgimap (p = 0.006). Yet, the mean difference was small (1.56± 6.20) (Table 2).
3. Intraobserver Variability
According to ICC, there was high agreement for both Oxford Cobbmeter and Surgimap. All readings were > 0.9 (Table 3).

Results of measurement variability by Oxford Cobbometer and Surgimap by the 2 observers showing high agreement for all readings (°) (n=123)
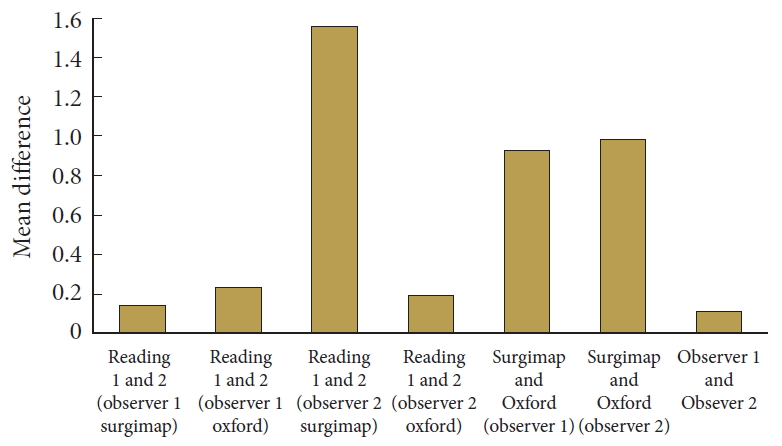
The mean intraobserver difference for the Oxford Cobbmeter was 0.24°± 3.35° for the observer 1 and 0.20°± 5.34° observer 2. As regards to the Surgimap, the mean intraobserver difference for observer 1and 2 were 0.10°± 3.12° and 1.56°± 6.20° respectively (Fig. 2).
4. Interobserver Variability
There was also high agreement for both Oxford Cobbometer and Surgimap. All readings were > 0.9 (Table 3). The mean difference between Surgimap and Oxford Cobbometer was 0.93°± 6.32° for observer 1 and 0.99°± 6.57° for observer 2 (Fig. 2).
5. Curve Classification Agreement
There was a good interobserver agreement for both methods for observers 1 and 2 (κ= 0.745, 0.693, respectively). Moreover, there was a very good interobserver agreement for Oxford Cobbometer (κ= 0.810) as well as Surgimap (κ= 0.804) methods (Table 4).
6. Measurement Time
We have used Bland-Altman test to analyze the time required by both observers to do measurements in each radiograph using both techniques (Fig. 3, Table 5).

The measurement time of both observers using Bland-Altman test. SD, standard deviation. *p≤0.05, statistically significant difference.
For observer 1, the mean time difference was statistically significant high (14.17± 22.93 seconds, p < 0.001), being less with the Oxford Cobbometer, meaning that he spent more significant time in doing measurements using the computer software. Again, with observer 2, the time spent using Cobbometer was less. However, the mean difference was not statistically significant. (0.32± 19.05 seconds, p = 0.878). Overall, poor agreement was observed.
Using paired t-test, the mean time taken by both using Surgimap was 38.3± 19.87 seconds (range, 12.67–111.5 seconds), versus 31.05±12.18 seconds (range, 12.50–72.50 seconds) using Cobbometer, which was statistically significant (p < 0.001).
DISCUSSION
Evaluation of the severity of scoliosis and its progression is often obtained from the Cobb angle measurement on standing long radiographs. Absolute difference of 5° in consecutive radiographs is typically indicative of curve progression. Therefore, accuracy is crucial in the Cobb angle measurement and management plan. The intraobserver and interobserver reliability and reproducibility of the Cobb measurement using different tools had been extensively reported [17-20].
Sources of measurement variability or errors are multiple and include an improper selection of one or both of the end vertebrae, and incorrect drawing of the lines through endplates or pedicles. A potential source of error includes also the level of experience of examiners. In addition, the magnitude of the curve could be a further potential source of error, being more with larger curves [21].
We have tried to eliminate the possible intrinsic sources of error in our study; we preselected the end vertebrae to avoid this error, and both observers were expert in treating spinal deformities. However, the 2 examiners were not familiar with one of both methods at the beginning, and met before the study to ensure that similar techniques were used. Observer 1 was using the Surgimap for the first time, and the same was true with the second observer for the Cobbometer.
Our results revealed a very satisfactory reliability and reproducibility of both Oxford Cobbometer and Surgimap computer software as methods of Cobb angle measurement. The interand intraobserver measurement agreement using both tools was high (according to ICC, all readings were > 0.9) (Table 3). Moreover, the mean differences in reading within or between observers were small; suggesting that there was small measurement bias between both methods. All of these were much less than the 5° difference which is the most widely accepted clinically significant difference in Cobb angle, and the threshold of changes that could influence treatment decisions.
Our mean differences are considered less than previously reported in other studies [9,12,14,22]. We were unable to explain that differences. However, our strategy for preselection of the end vertebrae as well as the level of experience of the observers could be factors in limiting difference bias.
We believe that the intraobserver variability is as important as the interobserver one, and both have important clinical implications. Significant intraobserver differences can lead to misdiagnosis of curve progression, thus influencing clinical treatment decisions as Carman et al. [19] noted. Moreover, Shaw et al. [23] reported that interobserver variability may be equally important in large public spinal clinics where the same clinician does not always assess the same patient.
Additionally, our curve classification agreement was also satisfactory. There was a good interobserver agreement for both methods (κ= 0.745, 0.693), and a very good interobserver agreement (κ= 0.810, 0.804) methods.
The mean Cobb angle in our study was 48.12°± 19.75° (range, 10.54°–110.76°) which is considered comparable or higher with the previous studies [7,9,12]. It should be also noted that we included a wide range of curves from the very mild to the most severe which represent the spectrum of patients attending specialized scoliosis clinics.
Few articles had addressed the Oxford Cobbmeter in Cobb angle measurements [9,12]. Our previous study revealed satisfactory reliability of the Oxford Cobbmeter compared to smartphone [9]. The advantages of the Oxford Cobbometer are that it is a quick and easy method. It precludes the use of protractors, wide-diameter markers, and lines on radiographs and so eliminates potential sources of intrinsic bias in measurement [12]. However, it requires a hard film for measurement. Based on our experience of several years of its use as well as previous studies confirming its validity, reliability, and reproducibility, we consider Oxford Cobbometer is the method of choice for manual Cobb angle measurements.
Several studies have evaluated digital radiology measurement. It has several advantages; including rapid comparison between radiographs, cheap storage and better visualization of the vertebral morphology. Different parts of the spine can be enlarged and seen more clearly by changing the contrast and enlargement, and the borders of the vertebrae can be enhanced by computerized options. After drawing lines along the endplates of end vertebrae, the software measures the angle automatically, which may reduce the intrinsic sources of error. Digital radiograph analysis become more common as the technology becomes increasingly popular and affordable [9,12,14,20,22,24,25].
When compared to the traditional method of measurement using protractor, Oxford Cobbometer demonstrates lower intraobserver variability in the study of Rosenfeldt et al. [12]. For the protractor method, intraobserver variability was 9.01° compared to 5.77° using the Cobbometer method.
A further systematic review of Langensiepen et al. [22] revealed high degrees of reliability for all of the measurement procedures including the manual and digital methods, with a slightly better tendency of the digital procedures over of manual ones.
Since the concepts of sagittal balance have gained increased focus, normal sagittal alignment restoration beside coronal correction is essential. Therefore, in addition to Cobb angle measurement, spinopelvic parameter including pelvic incidence, pelvic tilt, and sacral slope, etc. should be also evaluated [26]. We think that these parameters are better and easily evaluated by digital methods. A previous study by Wu et al. [14] using Surgimap software supported that.
Although digital radiography may not improve the measurement accuracy [25], it should be noted however that the present and future are inevitable with it especially with PACS which becomes widely used.
Little attention had been drawn towards the time spending in doing measurement. A reasonable timing is an important item in measurements, especially in busy public clinics. Our previous study revealed a good timing for measurement of 20 radiographs (1.25 minutes in the smartphone group compared to 1.29 minutes in the Oxford Cobbmeter group) [9]. Our results of the current study revealed significant differences in the measurement time using both techniques between the 2 observers, being less with Oxford Cobbometer. The mean time taken for a single radiograph measurement by the observer 1 using the Cobbomter was 29.73± 13.28 seconds (range, 9–82 seconds), compared to 43.91± 25.46 seconds (range, 11–142 seconds) using Surgimap. The mean time taken for observer 2 was 32.36± 14.7 seconds (range, 12–98 seconds) using the Cobbomter, compared to 32.68± 18.53 seconds (range, 9.73–100 seconds) when Surgimap was used. This means that the Cobbometer is quicker tool especially by the first senior author, and he spent significantly more time in the computer measurement. A finding that could be explained by the fact, that he was using that particular software for the first time. It should be noted however that the second observer was not familiar with Cobbometer at the beginning. Our previous findings further proved that Oxford Cobbmeter is a simple, reliable and quick tool with a short learning time.
The strength of the study is that it is to the best of our knowledge, the first report comparing Oxford Cobbmeter with computer digital Cobb angle measurement. The material was reasonable, with a wide range of curve severity. Including curve classification and measurement time could be further strength points.
The possible limitation in our study is that it included only 2 observers, and it would be better to expand the examiners to include also trainee or younger spine surgeons for more comprehensive evaluation.
CONCLUSION
The results of this study indicate that the Surgimap digital computer software measurement is an equivalent measuring tool to the Oxford Cobbometer in Cobb angle measurement. Both have high intra- and interobserver agreement for measurement and for curve classification, with small measurement differences. Oxford Cobbometer is advantageous in being quicker, and therefore it is the method of choice for manual measurement especially in developing countries where PACS or digital system facilities are not available.
Notes
The authors have nothing to disclose.